文中列举demo下载: (右键点击另存)
本文内容尽量通俗, 避免生僻术语, 主要偏重于原理, 里面的算法尽量简单, 建议先下载列举demo运行尝试
Demo 运行之后会在可执行文件工作目录下生成一张结果图(bmp格式)
1. 绘制一个点
把屏幕比喻成一个画布, 我们把画布上的某个点设置为某个颜色, 就达到目的了.
绘制一个点的核心代码:
|
1 2 3 4 5 6 7 |
void drawPoint(int* data, int width, int height, int pointX, int pointY, int color) { if(pointX >= 0 && pointX < width && pointY >= 0 && pointY < height) { data[pointX + pointY * width] = color; } } |
Demo 查看: point.cpp 里面用到一个 叫
void saveWithBMP_RGBA(const void* bitmapData, int w, int h, const char* filename);的函数将绘制结果保存到一个bmp 文件中方便查看绘制结果, 下面的Demo 也是如此, 不在赘述
2. 绘制一条线
瞎思考:
- 如果两个点在一条水平线或者竖直线上, 一次循环画点即可完成
- 如果这条直线y方向上的增量小于x方向上的增量, 是否可以在循环画点的时候给 y 乘以一个系数
- 同上, 如果这条直线y方向上的增量小于x方向上的增量, 是否可以以y方向循环画点, x 乘以一个系数
- 参考某些经典算法如
DDA,Bresenham等
代码样例1:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
// 按上面水平或者竖直方向递增的方式 瞎杰宝写的 void line(int* data, int width, int height, Point px, Point py, int color) { if(abs(px.x - py.x) < abs(px.y - py.y)) { if(px.y > py.y) { std::swap(px, py); } float dx = (py.x - px.x) / (float)(py.y - px.y); float x = px.x; int fromY = MAX(px.y, 0); int toY = MIN(py.y, height); for(; fromY <= toY; fromY += 1) { x += dx; drawPoint(data, width, height, x + 0.5, fromY, color); } } else { if(px.x > py.x) { std::swap(px, py); } float dy = (py.y - px.y) / (float)(py.x - px.x); float y = px.y; int fromX = MAX(px.x, 0); int toX = MIN(py.x, width); for(; fromX <= toX; fromX += 1) { y += dy; drawPoint(data, width, height, fromX, y + 0.5, color); } } } |
代码样例2:
上面的瞎写的代码稍微优化一下得到:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
void line(int* data, int width, int height, Point px, Point py, int color) { float dx = px.x - py.x; float dy = px.y - py.y; float len = sqrtf(dx * dx + dy * dy); float halfLen = len / 2; float centerX = (px.x + py.x) * 0.5f; float centerY = (px.y + py.y) * 0.5f; dx /= len; dy /= len; for(float f = 0; f < halfLen; f += 1.0f) { drawPoint(data, width, height, centerX + dx * f + 0.5f, centerY + dy * f + 0.5f, color); drawPoint(data, width, height, centerX - dx * f + 0.5f, centerY - dy * f + 0.5f, color); } } |
Demo 查看: line.cpp. 有兴趣的同学可以网上另外找一些经典算法, 会有很多优化手段, 这里随意写的, 看看效果就行.
3. 绘制&填充三角形
瞎思考:
- 如果我们要画一个不旋转的矩形, 我们会怎么画呢? 是否几个循环画一下线就完事?
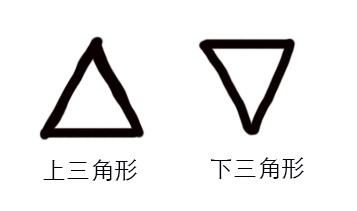
- 如果一个三角形是标准的上三角或者下三角呢 ?
是否有一个大胆的想法:
在有限的画布像素中, 我们从上往下可以把它看成一堆直线连接起来的图形?
根据这个方法可以写出代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
struct Point { int x, y; }; // 平顶/平底三角形, v0.y == v2.y, v1.y 最大 static inline void fillSimpleTriangle(int* data, int width, int height, const Point& v0, const Point& v1, const Point& v2, int color) { assert(v0.y == v2.y); float h = v1.y - v0.y; float dL = (v1.x - v0.x) / h; float dR = (v1.x - v2.x) / h; float xL = v0.x, xR = v2.x; if(v0.y < v1.y) { for(int i = v0.y; i <= v1.y; ++i) { line(data, width, height, xL, xR, i, color); //A Simple Function That Just Draw A Line xL += dL; xR += dR; } } else { for(int i = v0.y; i >= v1.y; --i) { line(data, width, height, xL, xR, i, color); //A Simple Function That Just Draw A Line xL -= dL; xR -= dR; } } } |
示例代码: triangle0.cpp
- 如果一个三角形不是上三角或者下三角呢 ?
我们可以将这类三角形分成上下两个部分, 然后就形成了两个满足条件的三角形
示例代码: triangle1.cpp示例图:
4. 绘制&填充多边形
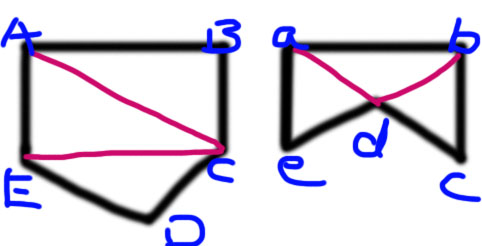
通常一个平面包含很多个顶点, 例:
如上图, 总共有十个顶点 A,B,C,D,E, a,b,c,d,e (对应索引 0 ~ 9)
我们根据这十个顶点, 然后给定索引就可以让它们以三角形的形式连接成我们想要的几何形状了.
比如上图, 我们只需要给定索引如下即可
|
1 2 3 4 5 6 7 8 9 10 |
{ 0, 1, 2, // △ABC 0, 2, 4, // △ACE 2, 3, 4, // △CDE 5, 6, 8, // △abd 6, 7, 8, // △bcd 5, 8, 9 // △ade } |
之后根据索引给出的顺序, 绘制上面列举的所有三角形, 即可完成多边形的绘制, 这里就不单独撸demo了. 请发散思维, 根据前面给出的demo实现多边形填充
5. 颜色填充
5.1 点和线 颜色填充
- 单个像素点颜色填充: 上面例子已经有了, 直接把那个像素设置为给定的颜色即可
- 线颜色填充: 纯色填充上面已经有例子了, 如果是渐变色填充, 取两边顶点的颜色按距离进行插值即可
5.2 三角形颜色填充
瞎思考:
- 如果一个三角形是标准的上三角或者下三角呢 ？
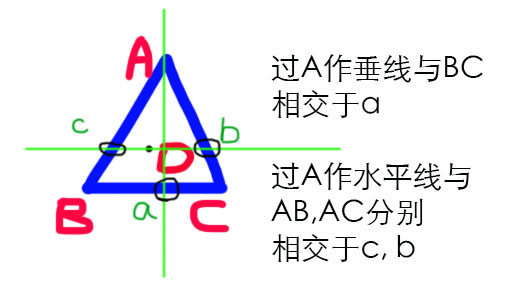如图描述, 我们依然可以转换为直线上的颜色计算, 我们可以通过 A、B 的颜色 算出 c 的颜色 同理可以计算得到 b 的颜色 有了 c 和 b 的颜色就够了 ! 有没有发现 c, D, b在一条水平线上? 是不是又转换成了一个已知问题 ? 于是对于 △ABC 内的任意一点像素的颜色, 就这样算出来了. - 如果是任意三角形呢 ?
参考上面任意三角形绘制原理哦
关键部分代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
// 平顶/平底三角形, v0[1] == v2[1], v1[1] 最大 inline void _fillSimpleTriangle(const Type& v0, const Type& v1, const Type& v2) { assert(v0[1] == v2[1]); float h = v1[1] - v0[1]; float dL = (v1[0] - v0[0]) / h; float dR = (v1[0] - v2[0]) / h; float xL = v0[0], xR = v2[0]; if(v0[1] < v1[1]) { Point p0 = v0; Point p1 = v2; for(int i = v0[1]; i <= v1[1]; ++i) { float percent = (i - v0[1]) / (float)(v1[1] - v0[1]); int c1 = mixColor(v0.color, v1.color, percent); int c2 = mixColor(v2.color, v1.color, percent); line(m_data, m_width, m_height, xL, xR, i, c1, c2); //A Simple Function That Just Draw A Line xL += dL; xR += dR; } } else { for(int i = v0[1]; i >= v1[1]; --i) { float percent = 1.0f - (i - v1[1]) / (float)(v0[1] - v1[1]); int c1 = mixColor(v0.color, v1.color, percent); int c2 = mixColor(v2.color, v1.color, percent); line(m_data, m_width, m_height, xL, xR, i, c1, c2); //A Simple Function That Just Draw A Line xL -= dL; xR -= dR; } } } |
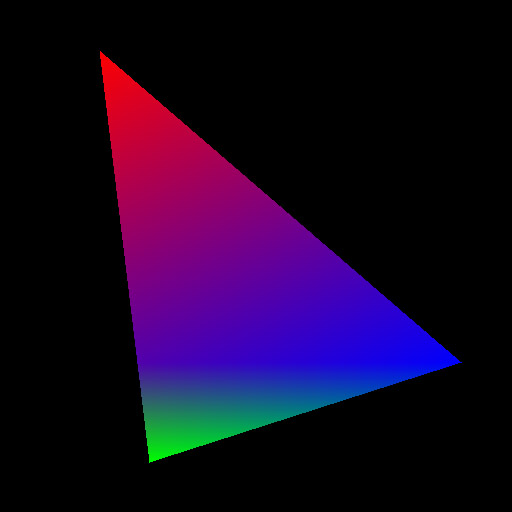
完整代码: triangle_color.cpp
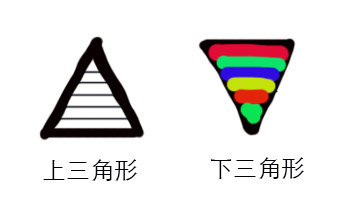
运行结果示例图:
文中列举demo下载:
本文链接: http://xege.org/draw_geometry_and_fill_colors.html
Author: wysaid
近期评论